🏷️ 그래프(Graph) 란?
요소들 간의 관계를 표현하는 망구조를 구현한 자료구조

구조
그래프 G 는 연결할 객체를 나타내는 정점(vertex)의 집합 V와 연결하는 간선(edge)의 집합 E로 구성되며, G = ( V , E )으로 표현할 수 있다.
- Vertex(정점) : 그래프의 기본 요소
- Edge (간선) : 정점과 정점을 연결하는 선
- Degree (차수) : 정점이 가지는 간선의 수
- 정점을 향하면 진입차수(in-degree)
- 정점에서 나가면 진출차수(out-degree)
- 방향 그래프에서 정점의 차수 = 진입차수 + 진출차수
- Path(경로) : 정점 a → b까지 간선을 따라 이동할때 만나는 정점을 순서대로 나열한 리스트
- 단순 경로 : 시작 정점과 끝 정점을 제외하고 정점을 중복으로 거치지 않는 경로
- Cycle(사이클) : 시작 정점과 끝 정점이 동일하면서 중복으로 거치는 정점이 없는 단순 경로
특징
- 응용 : 선형 자료구조나 트리가 표현할 수 없는 연결 구조들을 표현할 수 있기 때문에 다양한 분야에서 폭 넓게 사용할 수 있다. 대표적인 예로, 그래프는 네트워크를 나타내는 데 사용된다.
- 방향성 : 간선에 방향성이 있는가에 따라 방향성 혹은 무방향성 그래프로 나누어진다.
- 가중치 : 그래프에서 간선은 가중치를 가질 수 있다.
Graph vs Tree
Tree는 Graph 포함되는 형태로, 사이클이 없는 단순 연결 그래프 자료구조이다.
| 특징 | 그래프 (Graph) | 트리 (Tree) |
| 구조 |
정점(노드)과 간선으로 구성된 자료 구조
|
계층적 구조의 비선형 자료 구조
|
| 사이클 유무 | 사이클 가능 | 사이클 없음 |
| 루트 노드 | 루트 노드 없음 | 단말 루트 노드 |
| 연결성 | 모든 노드들이 연결되어 있거나 아닐 수 도 있음 | 모든 노드들이 연결 되어 있음 |
| 방향성 |
노드 간에 방향성이 있거나 없을 수도 있음
|
부모 → 자식 방향성을 가짐
|
| 하위 구조 |
여러 개의 연결 요소가 존재할 수 있음
|
하나의 루트 노드와 0개 이상의 하위 노드들로 구성됨
|
| 순회 |
일반적인 그래프 순회 방법 (BFS, DFS 등) 사용
|
in-order, pre-order, post-order 순회 방법 사용
|
🏷️ 그래프(Graph) 종류
Directed Graph ⟷ Undirected Graph
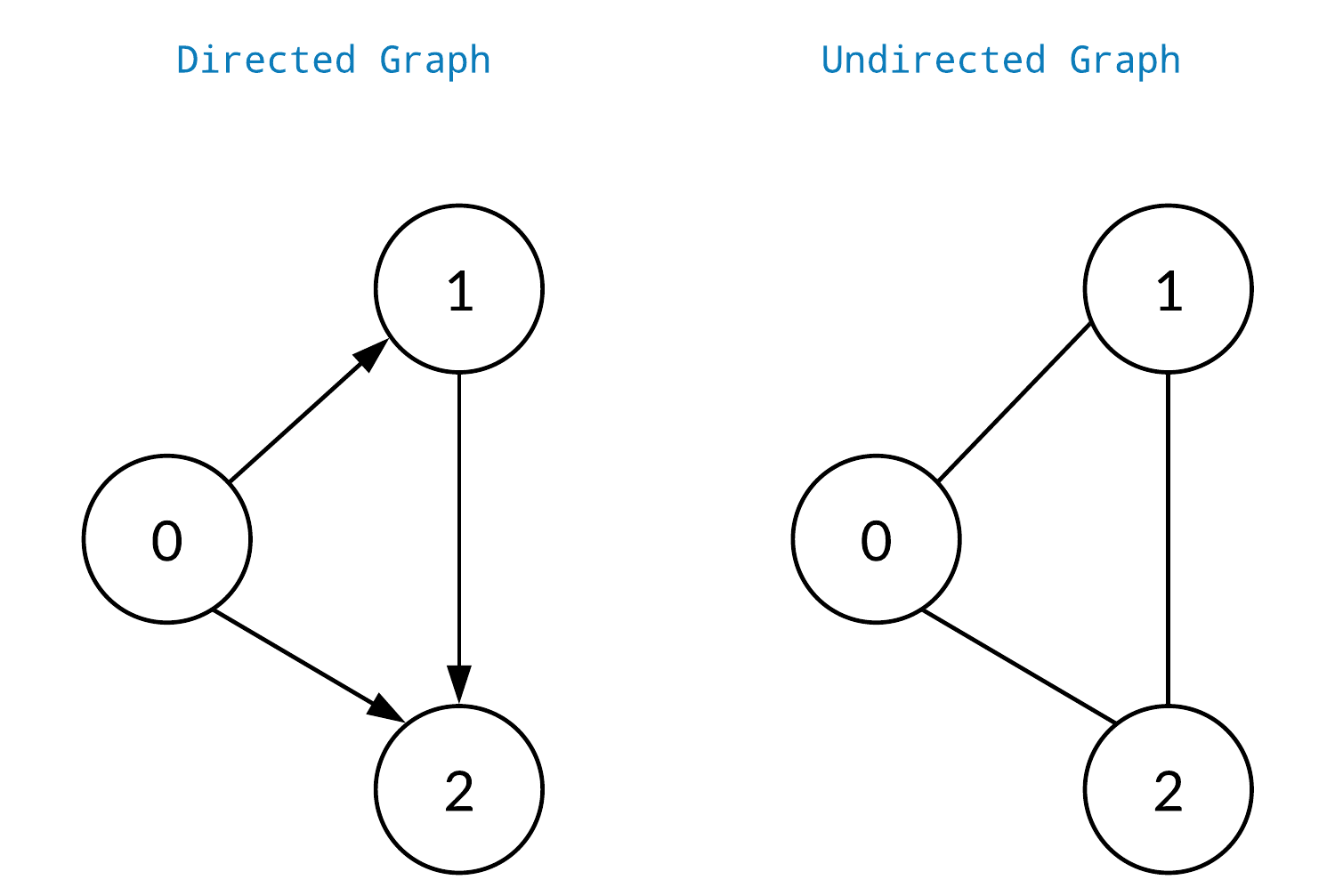
Directed Graph
방향 그래프는 간선에 방향이 있는 그래프를 말한다.
- 방향 그래프에서 간선은 a → b를 < a, b >라고 한다.
- < a, b >와 < b, a >는 서로 다른 간선으로 취급한다.
- 방향 그래프 G의 정점의 집합 V를 V(G) = { a, b }, 간선의 집합을 E(G) = { < a, b >,< b, a > }로 표현할 수 있다.
Undirected Graph
무방향 그래프는 간선에 방향이 없는 그래프를 말한다.
- 정점 a와 정점 b을 연결하는 간선을 ( a, b )로 표현한다.
- 방향이 없는 그래프이기에 ( a, b )와 ( b, a )는 같은 간선으로 취급한다.
- 무방향 그래프 G의 정점의 집합 V를 V(G) = { a, b }, 간선의 집합을 E(G) = { ( a, b ) }로 표현할 수 있다.
Cyclic Graph ⟷ Acyclic Graph

Cyclic Graph
사이클 그래프는 적어도 하나 이상의 사이클이 존재하는 그래프를 말한다.
Acyclic Graph
비사이클 그래프는 사이클이 존재하지 않는 그래프를 말한다.
Complete Graph ⟷ Subgraph Graph
Complete Graph
완전 그래프는 모든 정점들이 서로 연결되어 최대 간선 수를 가지는 그래프를 말한다.
- 무방향 그래프 : 정점이 n개이면, 최대 간선 수는 n x (n - 1) / 2 개
- 방향 그래프 : 정점이 n개이면, 최대 간선 수는 n x (n - 1) 개
Subgraph Graph
부분 그래프는 임의의 그래프에서 일부 정점과 간선으로 이루어진 그래프를 말한다.
Connected Graph ⟷ Disconnected Graph

Connected Graph
연결 그래프는 모든 정점들이 적어도 하나 이상의 경로를 가지는 그래프를 말한다
Disconnected Graph
비연결 그래프는 최소 하나 이상의 정점이 다른 정점과의 경로를 가지지 않는 그래프를 말한다.
Weight graph
가중치 그래프는 간선에 가중치를 할당하는 그래프로 네트워크라고도 말한다.
🏷️ 그래프(Graph) 구현
Adjacent Matrix
그래프를 2차원 배열로 구현하는 방법
N개의 정점을 가진 그래프를 구성하는 간선의 유무를 N x N 정방행렬로 표현한다. 이렇게 그래프를 표현한 행렬을 인접 행렬(Adjacent Matrix)이라고 한다.
- 자기자신을 향하는 간선(self-loop)은 없을 경우, 대각선을 항상 0 값을 가진다.
- 무방향 그래프 :
- 대각선을 중심으로 양쪽은 값이 항상 같기 때문에 대칭을 이룬다.
- 정점 index 차수 = 행 index 합 = 열 index 합
- 방향그래프
- 서로 다른 간선으로 취급하기 때문에, 대칭을 이루지 않는다.
- 정점 index 진출차수 = 행 index 합
- 정점 index 진입차수 = 열 index 합
- 간선의 개수에 상관없이 항상 N x N 개의 메모리를 사용하기 때문에 메모리 낭비 문제가 발생한다.
public class AdjacentMatrix{
private int matrix[][] = new int[10][10];
private int totalV = 0;
public void insertVertex(){
if (totalV < 10){
totalV++;
}
}
public void insertEdge(int val01, int val02){
if (val01 < totalV && val02 < totalV){
matrix[val01][val02] = 1;
}
}
public void printMatrix(){
for (int i = 0; i < totalV; i++){
for (int j = 0; j<totalV; j++){
System.out.printf("%2d", matrix[i][j]);
}
System.out.println();
}
}
}
Adjacent List
정점에 대한 인접 정점들을 Linked List로 구현하는 방법
N개의 정점을 가진 그래프를 정점 N 크기의 배열과 배열 요소에 해당 정점과 인접한 정점들을 리스트로 저장하여 표현한다. 이렇게 그래프를 표현한 리스트를 인접 리스트(Adjacent List)이라고 한다.
- 무방향 그래프
- 간선이 두 번 저장된다.
- N개의 정점과 E개의 간선을 가진 인접 리스트는 N개의 배열과 2E개의 노드가 필요하다.
- 방향그래프 : 정점의 진출차수가 인접한 정점들이다.
public class Graph{
private Node [] nodes; // node들을 저장할 배열
private static class Node {
int data;
boolean marked; // 방문 여부
LinkedList<Node> adjacent; // 인접한 node
Node(int data) {
this.data = data;
this.marked = false;
adjacent = new LinkedList<>();
}
}
public Graph(int size){
this.nodes = new Node[size];
for (int i = 0; i < size; i++) nodes[i] = new Node(i);
}
public void addEdge(int i1, int i2){
Node n1 = this.nodes[i1];
Node n2 = this.nodes[i2];
if (!n1.adjacent.contains(n2)) n1.adjacent.add(n2);
if (!n2.adjacent.contains(n1)) n2.adjacent.add(n1);
}
}
🏷️ 그래프(Graph) 탐색
Depth First Search
깊이 우선 탐색(DFS)은 시작 정점부터 시작하여 깊은 부분을 우선적으로 탐색하는 알고리즘
- Stack 혹은 재귀호출를 이용하여 구현한다.
- Tree의 경우, 루트 노드 부터 시작사여 단말노드까지 우선적으로 탐색한다.
- Tree 검색 방법이었던 inorder, preorder, postorder들도 DFS에 속한다.
Breadth First Search
너비 운선 탐색(BFS)은 시작 정점부터 시작하여 인접한 정점들을 우선적으로 탐색하는 알고리즘
- Queue을 이용하여 구현한다.
- Tree의 경우, level단위로 형제노드들을 차례로 우선적으로 탐색한다.
Reference
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] 해시 (Hash) (0) | 2023.07.29 |
|---|---|
| [자료구조] 신장 트리 (Spanning Tree) (0) | 2023.07.29 |
| [자료구조] 이진 힙 (Binary Heap) (0) | 2023.07.29 |
| [자료구조] 이진 검색 트리 (Binary Search Tree) (0) | 2023.07.29 |
| [자료구조] 트리 (Tree) (0) | 2023.07.29 |



